COMPSCI180_website
CS 180 Project 5
Project 5A
Part 0: Sampling from the Model
The objects instantiated above, stage_1 and stage_2, already contain code to allow us to sample images using these models. Read the code below carefully (including the comments) and then run the cell to generate some images. Play around with different prompts and num_inference_steps.


-
Prompt: “an oil painting of a snowy mountain village”
- Initial steps=20 output quality: The image is clear and detailed, accurately reflecting the style of an oil painting. The snowy mountain and village elements are well-represented.
- Different steps=50 output quality: There is no significant change in the image quality. The snowy mountain and village remain well-represented..
-
Prompt: “a man wearing a hat”
- Initial steps=20 output quality: The image is clear, and the man’s figure is well-defined, but some finer details are lacking.
- Different steps=50 output quality: The image quality improves, with richer details in the man’s features. The man’s face shows more wrinkles, adding to the realism.
-
Prompt: “a rocket ship”
- Initial steps=20 output quality: The image is clear, and the rocket ship is well-defined, but the background details are minimal.
- Different steps=50 output quality: The image quality improves, with more detailed and vibrant representation of the rocket ship. The background now shows more texture and patterns, adding depth to the scene.
Part 1: Sampling Loops
1.1: Implementing the forward process
A key part of diffusion is the forward process, which takes a clean image and adds noise to it. In this part, we will write a function to implement this. The forward process is defined by:
\[q(x_t | x_0) = N(x_t ; \sqrt{\bar\alpha_t} x_0, (1 - \bar\alpha_t)\mathbf{I})\tag{1}\]which is equivalent to computing \(x_t = \sqrt{\bar\alpha_t} x_0 + \sqrt{1 - \bar\alpha_t} \epsilon \quad \text{where}~ \epsilon \sim N(0, 1) \tag{2}\)
That is, given a clean image \(x_0\), we get a noisy image \(x_t\) at timestep \(t\) by sampling from a Gaussian with mean \(\sqrt{\bar\alpha_t} x_0\) and variance \((1 - \bar\alpha_t)\). Note that the forward process is not just adding noise – we also scale the image.
You will need to use the alphas_cumprod variable, which contains the \(\bar\alpha_t\) for all \(t \in [0, 999]\). Remember that \(t=0\) corresponds to a clean image, and larger $t$ corresponds to more noise. Thus, \(\bar\alpha_t\) is close to 1 for small \(t\), and close to 0 for large \(t\). Run the forward process on the test image with \(t \in [250, 500, 750]\). Show the results – you should get progressively more noisy images.

1.2: Classical Denoising
Let’s try to denoise these images using classical methods. Again, take noisy images for timesteps [250, 500, 750], but use Gaussian blur filtering to try to remove the noise. Getting good results should be quite difficult, if not impossible.

1.3 Implementing One Step Denoising
Now, we’ll use a pretrained diffusion model to denoise. The actual denoiser can be found at stage_1.unet. This is a UNet that has already been trained on a very, very large dataset of \((x_0, x_t)\) pairs of images. We can use it to recover Gaussian noise from the image. Then, we can remove this noise to recover (something close to) the original image. Note: this UNet is conditioned on the amount of Gaussian noise by taking timestep $t$ as additional input.
Because this diffusion model was trained with text conditioning, we also need a text prompt embedding. We provide the embedding for the prompt "a high quality photo" for you to use. Later on, you can use your own text prompts.

1.4 Implementing Iterative Denoising
In part 1.3, you should see that the denoising UNet does a much better job of projecting the image onto the natural image manifold, but it does get worse as you add more noise. This makes sense, as the problem is much harder with more noise!
But diffusion models are designed to denoise iteratively. In this part we will implement this.
In theory, we could start with noise \(x_{1000}\) at timestep \(T=1000\), denoise for one step to get an estimate of \(x_{999}\), and carry on until we get \(x_0\). But this would require running the diffusion model 1000 times, which is quite slow (and costs $$$).
It turns out, we can actually speed things up by skipping steps. The rationale for why this is possible is due to a connection with differential equations. It’s a tad complicated, and out of scope for this course, but if you’re interested you can check out this excellent article.
To skip steps we can create a list of timesteps that we’ll call strided_timesteps, which will be much shorter than the full list of 1000 timesteps. strided_timesteps[0] will correspond to the noisiest image (and thus the largest $t$) and strided_timesteps[-1] will correspond to a clean image (and thus \(t = 0\)). One simple way of constructing this list is by introducing a regular stride step (e.g. stride of 30 works well).
On the ith denoising step we are at \(t =\) strided_timesteps[i], and want to get to \(t' =\) strided_timesteps[i+1] (from more noisy to less noisy). To actually do this, we have the following formula:
where:
- $x_t$ is your image at timestep $t$
- $x_{t’}$ is your noisy image at timestep $t’$ where $t’ < t$ (less noisy)
- $\bar\alpha_t$ is defined by
alphas_cumprod, as explained above. - $\alpha_t = \bar\alpha_t / \bar\alpha_{t’}$
- $\beta_t = 1 - \alpha_t$
- $x_0$ is our current estimate of the clean image using equation 2 just like in section 1.3
The \(v_\sigma\) is random noise, which in the case of DeepFloyd is also predicted. The process to compute this is not very important for us, so we supply a function, add_variance, to do this for you.


1.5 Diffusion Model Sampling
In part 1.4, we use the diffusion model to denoise an image. Another thing we can do with the iterative_denoise function is to generate images from scratch. We can do this by setting i_start = 0 and passing in random noise. This effectively denoises pure noise. Please do this, and show 5 results of "a high quality photo".

1.6 Classifier Free Guidance
You may have noticed that some of the generated images in the prior section are not very good. In order to greatly improve image quality (at the expense of image diversity), we can use a technique called Classifier-Free Guidance.
In CFG, we compute both a noise estimate conditioned on a text prompt, and an unconditional noise estimate. We denote these $\epsilon_c$ and \(\epsilon_u\). Then, we let our new noise estimate be
\[\epsilon = \epsilon_u + \gamma (\epsilon_c - \epsilon_u) \tag{4}\]where \(\gamma\) controls the strength of CFG. Notice that for \(\gamma=0\), we get an unconditional noise estimate, and for \(\gamma=1\) we get the conditional noise estimate. The magic happens when \(\gamma > 1\). In this case, we get much higher quality images. Why this happens is still up to vigorous debate. For more information on CFG, you can check out this blog post.
Please implement the iterative_denoise_cfg function, identical to the iterative_denoise function but using classifier-free guidance. To get an unconditional noise estimate, we can just pass an empty prompt embedding to the diffusion model (the model was trained to predict an unconditional noise estimate when given an empty text prompt).
Disclaimer
Before, we used "a high quality photo" as a “null” condition. Now, we will use the actual "" null prompt for unconditional guidance for CFG. In the later part, you should always use "" null prompt for unconditional guidance and use "a high quality photo" for unconditional generation.

1.7 Image-to-image Translation
In part 1.4, we take a real image, add noise to it, and then denoise. This effectively allows us to make edits to existing images. The more noise we add, the larger the edit will be. This works because in order to denoise an image, the diffusion model must to some extent “hallucinate” new things – the model has to be “creative.” Another way to think about it is that the denoising process “forces” a noisy image back onto the manifold of natural images.
Here, we’re going to take the original test image, noise it a little, and force it back onto the image manifold without any conditioning. Effectively, we’re going to get an image that is similar to the test image (with a low-enough noise level). This follows the SDEdit algorithm.
To start, please run the forward process to get a noisy test image, and then run the iterative_denoise_cfg function using a starting index of [1, 3, 5, 7, 10, 20] steps and show the results, labeled with the starting index. You should see a series of “edits” to the original image, gradually matching the original image closer and closer.


1.7.1 Editing Hand-Drawn and Web Images
This procedure works particularly well if we start with a nonrealistic image (e.g. painting, a sketch, some scribbles) and project it onto the natural image manifold.
Please experiment by starting with hand-drawn or other non-realistic images and see how you can get them onto the natural image manifold in fun ways.
We provide you with 2 ways to provide inputs to the model:
- download images from the web
- draw your own images
Please find an image from the internet and apply edits exactly as above. And also draw your own images, and apply edits exactly as above. Feel free to copy the prior cell here. For drawing inspiration, you can check out the examples on this project page.






1.7.2 Inpainting
We can use the same procedure to implement inpainting (following the RePaint paper). That is, given an image \(x_{orig}\), and a binary mask \(\bf m\), we can create a new image that has the same content where \(\bf m\) is 0, but new content wherever \(\bf m\) is 1.
To do this, we can run the diffusion denoising loop. But at every step, after obtaining \(x_t\), we “force” $x_t$ to have the same pixels as $x_{orig}$ where \(\bf m\) is 0, i.e.:
\[x_t \leftarrow \textbf{m} x_t + (1 - \textbf{m}) \text{forward}(x_{orig}, t) \tag{5}\]Essentially, we leave everything inside the edit mask alone, but we replace everything outside the edit mask with our original image – with the correct amount of noise added for timestep $t$.




1.7.3 Text-Conditioned Image-to-image Translation
Now, we will do the same thing as the previous section, but guide the projection with a text prompt. This is no longer pure “projection to the natural image manifold” but also adds control using language. This is simply a matter of changing the prompt from "a high quality photo" to any of the precomputed prompts we provide you (if you want to use your own prompts, see appendix).

1.8 Visual Anagrams
In this part, we are finally ready to implement Visual Anagrams and create optical illusions with diffusion models. In this part, we will create an image that looks like "an oil painting of an old man", but when flipped upside down will reveal "an oil painting of people around a campfire".
To do this, we will denoise an image $x_t$ at step $t$ normally with the prompt "an oil painting of an old man", to obtain noise estimate $\epsilon_1$. But at the same time, we will flip $x_t$ upside down, and denoise with the prompt "an oil painting of people around a campfire", to get noise estimate $\epsilon_2$. We can flip $\epsilon_2$ back, to make it right-side up, and average the two noise estimates. We can then perform a reverse diffusion step with the averaged noise estimate.
The full algorithm is:
\[\epsilon_1 = \text{UNet}(x_t, t, p_1)\] \[\epsilon_2 = \text{flip}(\text{UNet}(\text{flip}(x_t), t, p_2))\] \[\epsilon = (\epsilon_1 + \epsilon_2) / 2\]where UNet is the diffusion model UNet from before, \(\text{flip}(\cdot)\) is a function that flips the image, and $p_1$ and $p_2$ are two different text prompt embeddings. And our final noise estimate is \(\epsilon\). Please implement the above algorithm and show example of an illusion.



1.9 Hybrid Images
In this part we’ll implement Factorized Diffusion and create hybrid images just like in project 2.
In order to create hybrid images with a diffusion model we can use a similar technique as above. We will create a composite noise estimate \(\epsilon\), by estimating the noise with two different text prompts, and then combining low frequencies from one noise estimate with high frequencies of the other. The algorithm is:
\[\epsilon_1 = \text{UNet}(x_t, t, p_1)\] \[\epsilon_2 = \text{UNet}(x_t, t, p_2)\] \[\epsilon = f_\text{lowpass}(\epsilon_1) + f_\text{highpass}(\epsilon_2)\]where UNet is the diffusion model UNet, \(f_\text{lowpass}\) is a low pass function, \(f_\text{highpass}\) is a high pass function, and \(p_1\) and \(p_2\) are two different text prompt embeddings. Our final noise estimate is \(\epsilon\). Please show an example of a hybrid image using this technique (you may have to run multiple times to get a really good result for the same reasons as above). We recommend that you use a gaussian blur of kernel size 33 and sigma 2.



Project 5B: Training Your Own Diffusion Model!
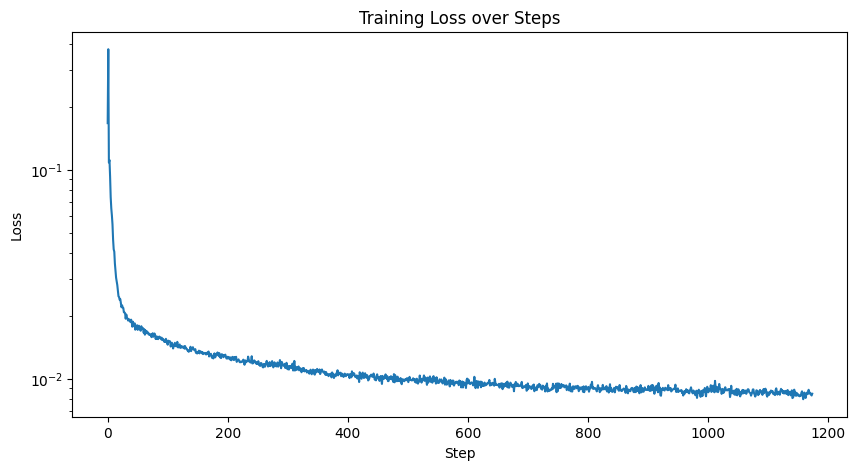
Part 1: Training a Single-step Denoising UNet



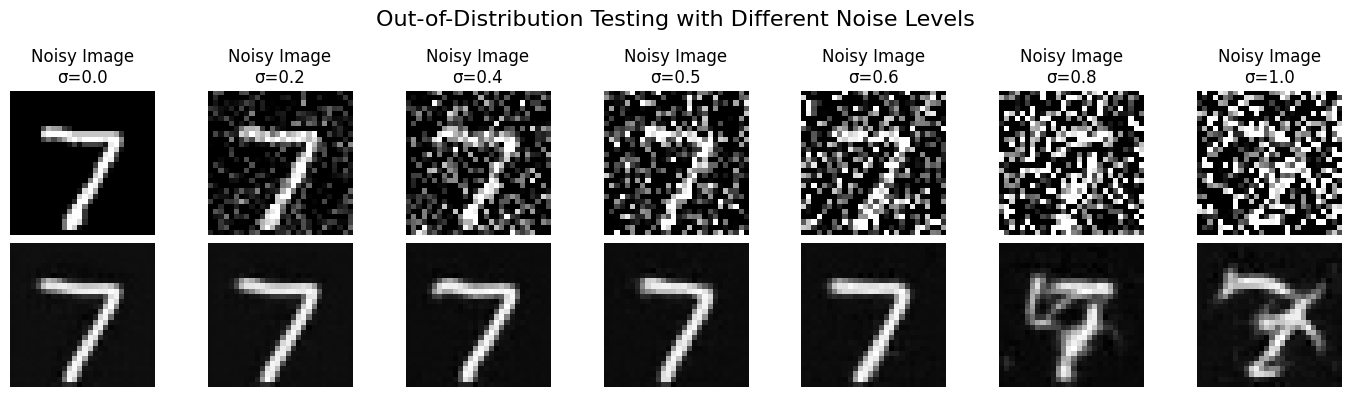
Part 2: Training a Diffusion Model
1. Implementing a Time-conditioned UNet
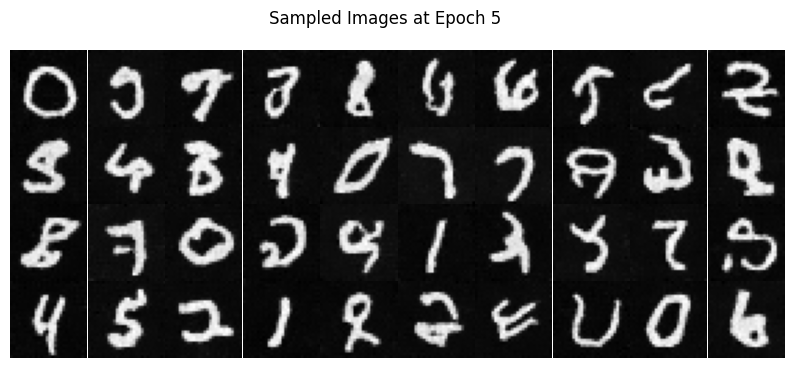

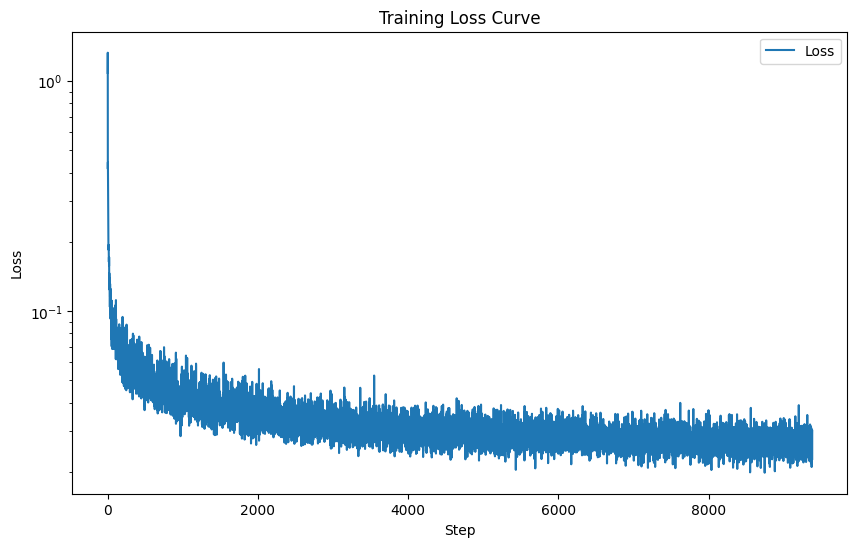
2. Implementing class-conditioned UNet